Language Described by Nfa Using Table
Concatenation of 3 and b. Concatenation of 5 and b.

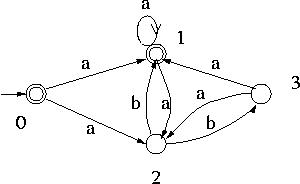
Nfa Of Regular Language L Ab Ba Geeksforgeeks
B Prove that the NFA accepts the language described in a using induction on the length of the input.
. We give six definitions of the regular languages. Assuming R then R describes the language and to prove that it is regular we construct an NFA M QΣ. The finite automata are called NFA when there exist many paths for specific input from the current state to the next state.
3 is false the DFA can be minimized to two states. For NFA has properties similar to that for DFA. The machine accepts only if it ends with.
The definition below from the paper Reducing the size of NFAs by using equivalences and preorders by Ilie et al. L a n b m n 0 m 0 and n m Pumping Lemma. Suppose that C is a language recognized by some NFA M ie C LM.
We will find equivalent pairs of states in an NFA by using their definition. DFA NFA ε-NFA Equivalence Surprisingly enough εtransitionsto our NDFA does NOT give it any additional language accepting power. For the language accepted by A A is the minimal DFA.
And the language it accepts is a ab a ba bb. I dont know if your searching for an explanation in terms of how can one lead to a solution like this or if you want a proof about this NFA accepting that language. So the language accepted by your NFA ought to be something of the form L b l b a h b b i b a j a b k b i j k l h 0 Ive given a quasi-final form of the language.
Q is null in the starting. Add transitions of the start state to the transition table T. Hence we will add the inputs 0s and 1s so that the substring 1010 of the language can be maintained.
Thats what well try to do here. Initially Q ɸ. L A is regular its complement would also be regular.
The induction hypothesis is given by Hn for all strings w of length n the following three statements are true. Using deterministic finite automata DFAs. If it sees a b before an a it crashes.
Construct the NFA for abab bab. L A L 1100 0 101 3. In each part of the below figure is pictured an NFA.
It is easy to construct an NFA than DFA for a given regular language. One with states and the other with states The language of can be described by the regular language given by this regular expression We define using ε-moves but can be defined without using ε-moves. Each regular language can be compactly described using a regular expression.
For each state in Q find the possible set of states for each input symbol using transition function of NFA. Can be viewed as the union of two DFAs. It can see any number of b but after the initial run of a it can never again see two a in a row.
Then the DFA D Q q0 δ F can be constructed for language L as. Informally two states are right equivalent if for all input strings they reach the same sets. A accepts all strings over 0 1 of length at least 2.
B Consider the DFA M q9293 018993 where 8 is defined in the table below. 38 Chapter 3 of Martin. Now as 1010 could be the substring.
By problem 3 on Homework 2 we then know there is another DFA D that recognizes the language LD. The partial transition diagram can be. Add start state of the NFA to Q.
Use the algorithm described in the proof of Theorem 317 Lecture 3 to draw an NFA with no Λ-transitions accepting the same languageExercise 7 Ex. Here is a table of REs and the languages they denote. This is a NFA with 3 states that accepts that exact language.
Construct the NFA for abab. Construct the NFA for ba. Using nondeterministic finite automata NFAs.
Let T be a new transition table of the DFA. Construct an NFA that accepts the same language using the construction algorithm given in Lemma 155 of the textbook. Every NFA is not DFA but each NFA can be translated into DFA.
Is this language L over the alphabet a b regular. We obtain this NFA by defining Q q q the start state F q and δq a State diagram of M. Suppose there is an NFA N Q q0 δ F which recognizes a language L.
Let Q be a new set of states of the DFA. A Consider the regular language described by the regular expression R 0 U 110 u 1. We use mutual induction on the three states and their properties.
To show NFA-ε is equivalent to NFA first note that NFA is a special case of NFA-ε so it remains to show. Some of the strings accepted by the NFA given above are a ab aaa abbbb etc. The opposite of this language is L R E G L.
The language consists of all the string containing substring 1010. The language accepted by an NFA Q q 0 A is the set of strings that are accepted by the NFA. Add q0 to Q.
Using a closure definition involving union concate-nation and Kleene. Concatenation of b and a. Assuming R ϵ then R describes the language ϵ and to prove that it is regular we shall construct a NFA M QΣ δ q F that accepts this language.
It will also be essential when showing the Fas accept the class of Regular Languages. After that if it sees at least one b it can accept. Hence the NFA becomes.
1 A Aw. 2 B Aw w ends with a 1. Your NFA loops in q0 accepting any number of a until it sees at least one a.
NFA Non-Deterministic finite automata NFA stands for non-deterministic finite automata. Transition table for the above transition diagram can be given below. Defines what it means for two states to be right equivalent.
Xis in the language recognized by an NFA if. Union of 4 and 6 More Text Exercises. Each regular expression can be systematically translated into an NFA.
DFAs NFAs Regular Languages The family of regular languages is the simplest yet inter-esting family of languages. Can prove as follows. Nondeterministic Finite Automata NFA Graph with start state final states edges labeled by symbols like DFA but Not required to have exactly 1 edge out of each state labeled by each symbol---can have 0 or 1 Also can have edges labeled by empty string ε Defn.
Create an ε-NFA for the language described by the expression than it is to create a plain old DFA. Construct the NFA for bab. Since every NFA has an equivalent DFA Theorem 139 there is a DFA D such that LD LM C.
Converting NFA to DFA- The following steps are followed to convert a given NFA to a DFA- Step-01. Since youll know how to convert languages to NFA in this sequel I dispense with drawing the NFAs for these REsbut you are. A regular language is also context free.

Nfa Of Regular Language L 0 1 00 11 And L B Ba Geeksforgeeks
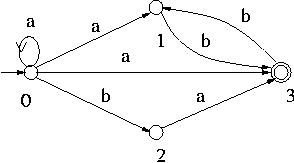
Comments
Post a Comment